Before you get started, take this readiness quiz.
In this section, we will examine this type of revolving motion around a circle. To do so, we need to define the type of circle first, and then place that circle on a coordinate system. Then we can discuss circular motion in terms of the coordinate pairs.
To define our trigonometric ratios, we begin by drawing a unit circle (a circle of radius \(1\) centered at the origin \((0,0)\)).
Recall that the x- and y-axes divide the coordinate plane into four quarters called quadrants. We label these quadrants to mimic the direction a positive angle would sweep. The four quadrants are labeled I, II, III, and IV.
For an acute angle \(t,\) we can label the intersection of the terminal side and the unit circle as by its coordinates, \((x,y)\). Since the circle has radius \(1\), using our trigonometric ratios we see that the triangle in orange below has base \(\cos t\) and height \(\sin t\). The coordinates \(x\) and \(y\) therefore can be related to the angle \(t\): \(x= \cos t\) and \(y= \sin t\). Also, \(\tan t=\dfrac\).
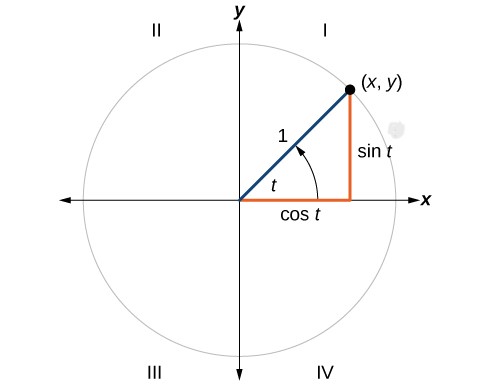
A unit circle has a center at \((0,0)\) and radius \(1\). Form the angle with measure \(t\) with initial side coincident with the \(x\)-axis.
Let \((x,y)\) be point where the terminal side of the angle and unit circle meet. Then \((x,y)=(\cos t,\sin t)\). Further, \(\tan t=\dfrac\).
Now that we have our unit circle labeled, we can learn how the \((x,y)\) coordinates relate to the angle \(t\). For an acute angle, the sine ratio \(\sin t\) is the \(y\)-coordinate of the point where the corresponding terminal side of the angle intersects the unit circle and the cosine ratio \(\cos t\) is the \(x\)-coordinate of the point where the corresponding terminal side of the angle intersects the unit circle. We extend this definition to all angles. So, we define the sine ratio \(\sin t\) to be the \(y\)-coordinate of the point where the corresponding terminal side of the angle intersects the unit circle and the cosine ratio \(\cos t\) to be the \(x\)-coordinate of the point where the corresponding terminal side of the angle intersects the unit circle. The tangent ratio \(\tan t\) is \(\dfrac\).
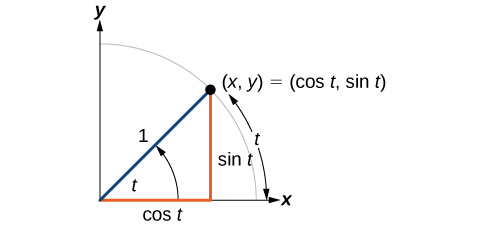
We may enclose the angle in parentheses or not depending on how clear the expression is: \(\sin t\) is the same as \(\sin (t)\) and \(\cos t\) is the same as \(\cos (t)\). When in doubt, use the extra parentheses when entering calculations into a calculator or computer.
SINE, COSINE, and TANGENT RATIOS
If \(t\) is an angle measurement and a point \((x,y)\) is both on the unit circle and the terminal side of the angle in standard position, then
\[ \begin \cos t & = x \\ \sin t & = y \\ \tan t &=\dfrac\end\]
Solution
Moving \(90^>\) counterclockwise around the unit circle from the positive \(x\)-axis brings us to the top of the circle, where the \((x,y)\) coordinates are \((0,1)\), as shown here:
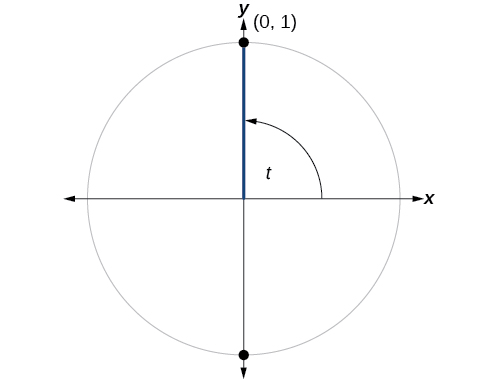
Using our definitions of cosine and sine,
\(\begin x &= \cos t = \cos (90^>) = 0 \\ y &= \sin t = \sin (90^>) = 1 \end \)
The cosine of \(90^>\) is 0; the sine of \(90^>\) is 1.
Try It \(\PageIndex\)
Find cosine and sine of the angle \(\pi\).
Answer
Now that we can define sine and cosine, we will learn how they relate to each other and the unit circle. Recall that the equation for the unit circle is \(x^2+y^2=1\). Because \(x= \cos t\) and \(y=\sin t\), we can substitute for \( x\) and \(y\) to get \(\cos ^2 t+ \sin ^2 t=1.\) This equation, \( \cos ^2 t+ \sin ^2 t=1,\) is known as the Pythagorean Identity. See below:
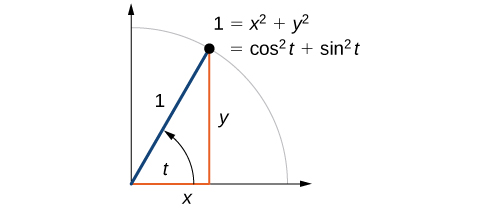on the unit circle. And equation showing the equivalence of 1, x^2 + y^2, and cos^2 t + sin^2 t. " width="487px" height="210px" />
We can use the Pythagorean Identity to find the cosine of an angle if we know the sine, or vice versa. However, because the equation yields two solutions, we need additional knowledge of the angle to choose the solution with the correct sign. If we know the quadrant where the angle is, we can easily choose the correct solution.
The Pythagorean Identity states that, for any angle \(t\),
How To: Given the sine of some angle t and its quadrant location, find the cosine of t
If \(\sin (t)=\dfrac\) and \(t\) is in the second quadrant, find \( \cos (t)\).
Solution
If we drop a vertical line from the point on the unit circle corresponding to \(t\), we create a right triangle, from which we can see that the Pythagorean Identity is simply one case of the Pythagorean Theorem.
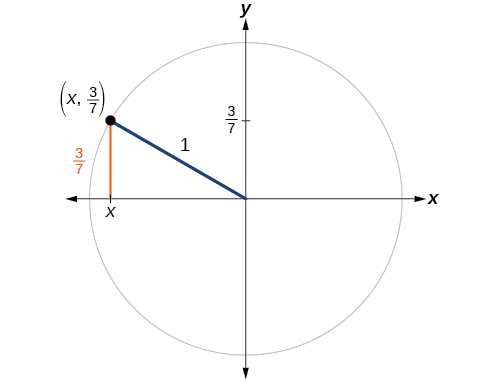
Substituting the known value for sine into the Pythagorean Identity,
Because the angle is in the second quadrant, we know the \(x\)-value is a negative real number, so the cosine is also negative. So
Try It \(\PageIndex\)
If \(\cos (t)=\dfrac\) and \(t\) is in the fourth quadrant, find \( \sin (t)\).
Answer
When possible, we would like to be precise about evaluation of the sine and cosine ratios. We give an example here.
a) Find the value of \(\sin 150^\text\)
b) Find the value of \(\cos\dfrac<7\pi>\).
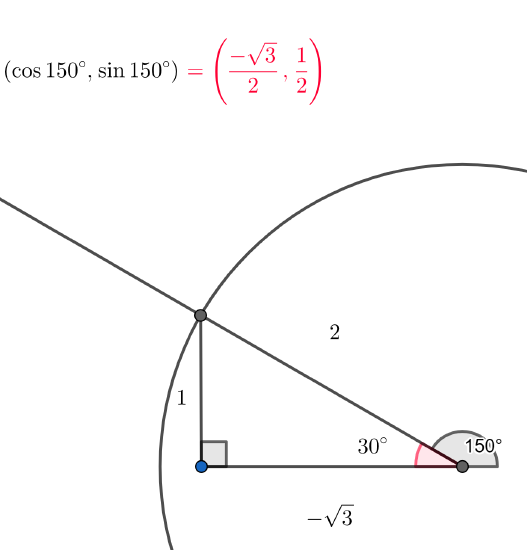
a) We first draw a picture and identify a triangle (while there are two natural possibilities, we will use the triangle shown below (often called "the reference triangle)).
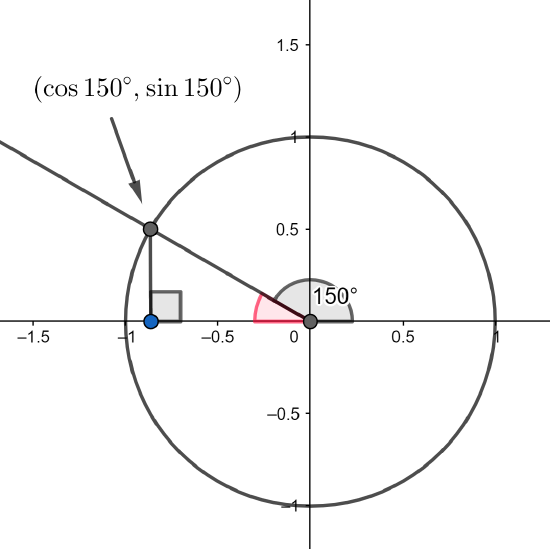
Then determine the reference angle indicated in red. To do this we note that the straight angle (black angle plus the red angle is \(180^\text\). So the red angle measures \(30^\text\). Then we use our knowledge of the 30-60-90 triangle (choosing the one with hypotenuse 1) and note the lengths on the diagram.
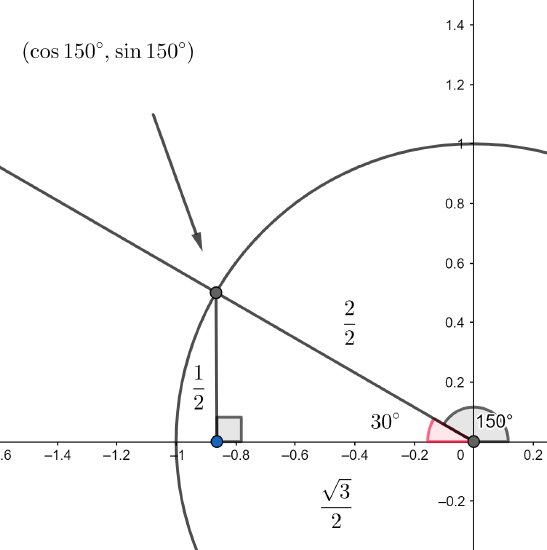
Finally, making note of the position of the triangle, we see that the \(x\)-coordinate must be negative and the \(y\)-coordinate must be positive, we find
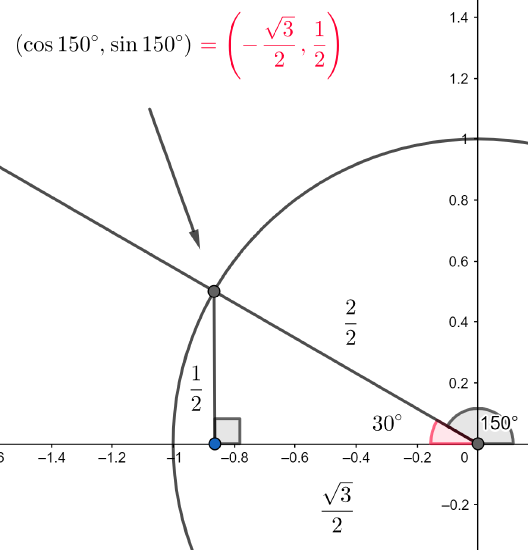
So we conclude, in particular, that \(\sin 150^\text=\dfrac12\).
Note that we could also use the standard triangle (using the circle of radius 2) and use signed lengths and form the sine ratio as before:
b) We first draw the angle together with the unit circle and label the intersection:
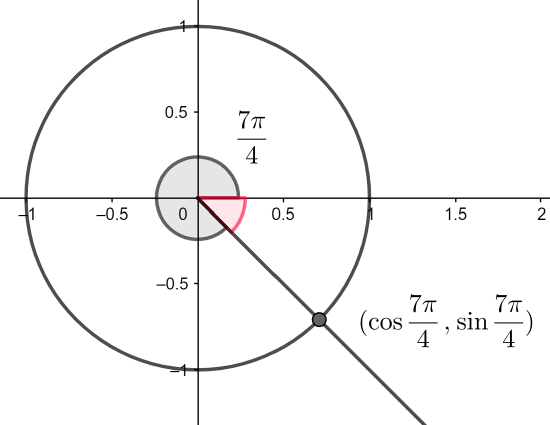
We determine the value of the red angle (noting that the black angle plus the red angle measures \(2\pi\). We construct a right triangle that will help us determine the coordinates of the labeled intersection (here we will use, again, what is often called 'the reference triangle').
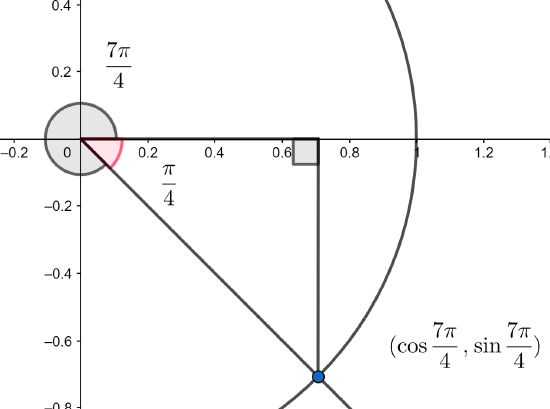
Now, we recall the 45-45-90 triangle from memory (or rederive it) and scale it to have the hypotenuse have length 1.
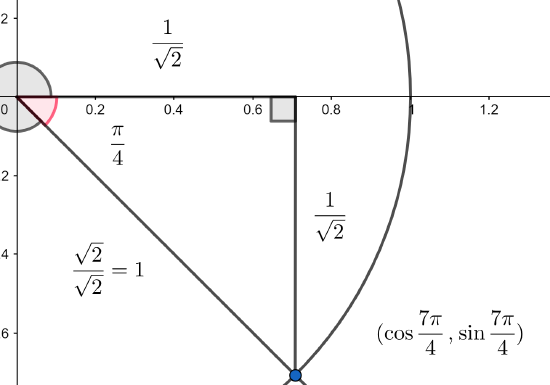
Now, we note from the location of the point that the \(x\)-coordinate must be positive and the \(y\)-coordinate must be negative. We determine the coordinates of the labeled intersection.
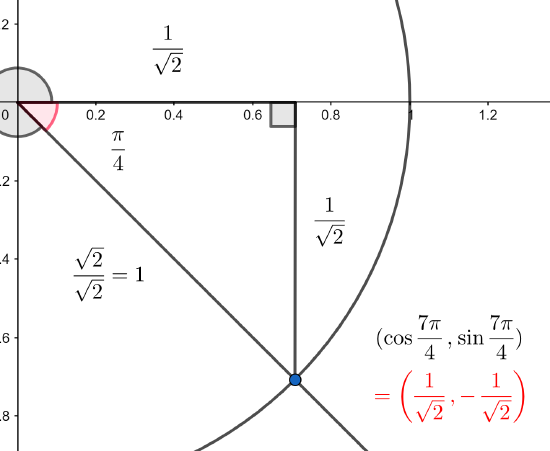
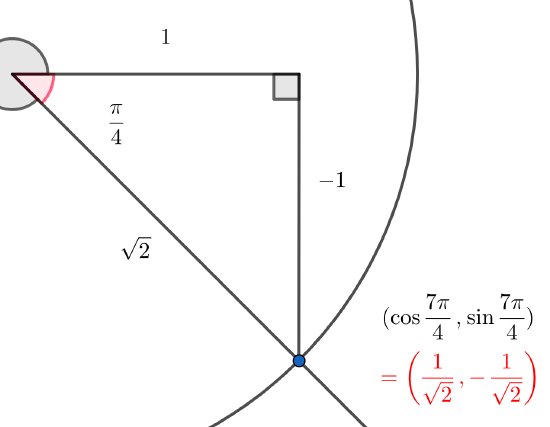
As in part a) we could also use the standard triangle (using the circle of radius 2) and use signed lengths and form the sine ratio as before:
To find a reference angle, draw a sketch noting in which quadrant your terminal side is and use your familiarity with right angles and straight angles to figure out the reference angle. Try these exercises using the above example as a model.
Find the value of
c) \(\tan 225^\text\) (Here use the extension that \(\tan t=\dfrac.\)
Answer
To find the cosine and sine of angles other than the special angles, we turn to a computer or calculator. Be aware: Most calculators can be set into “degree” or “radian” mode, which tells the calculator the units for the input value. When we evaluate \( \cos (30^\text)\) on our calculator, it will evaluate it as the cosine of 30 degrees if the calculator is in degree mode, or the cosine of 30 radians if the calculator is in radian mode.
Example \(\PageIndex\): Using a Graphing Calculator to Find Sine and Cosine
a) Evaluate \( \sin 150^\text\) using a calculator or computer.
b) Evaluate \(\cos \dfrac<7\pi>\)
Solution
a) This depends on your calculator. But we know the answer is \(\dfrac12\). Make sure the mode on the calculator is set to 'degree'.
b) This depends on your calculator. But we know the answer is \(\dfrac>\) so if you square your answer you should get \(\dfrac12\) and your answer should be positive. Make sure the mode on the calculator is set to 'radian'.
Try It \(\PageIndex\)
Evaluate \(\sin (-50)\).
Answer
Evaluate \(\cos(-210^>)\) and \(\sin(-210^>)\). Support your answer with an appropriate picture of the unit circle. Then evaluate \(\tan(210^>)\).
This page titled 4.1.4: The Unit Circle is shared under a CC BY 4.0 license and was authored, remixed, and/or curated by Holly Carley and Ariane Masuda via source content that was edited to the style and standards of the LibreTexts platform.
